Integral Tertentu
1. Pengertian Integral sebagai Luas Suatu Bidang Datar
Kalian pasti sudah pernah mempelajari perhitungan luas bangun datar.
Bangun datar apa saja yang sudah kalian kenal? Bangun datar yang kalian
kenal pasti merupakan bangun datar beraturan, misalnya segitiga, segi
empat, lingkaran, dan sebagainya.
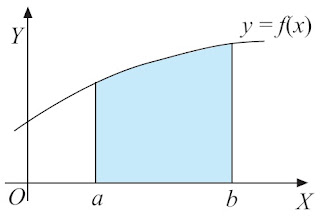 |
| Gambar 2. Bangun datar yang dibatasi kurva y = f(x), sumbu X, serta garis x = a dan y = b. |
Perhatikan Gambar 2. Apakah gambar daerah yang diarsir tersebut merupakan bangun datar yang sudah kalian kenal?
Termasuk bangun apakah gambar daerah tersebut? Dapatkah kalian
menentukan luas bangun datar tersebut dengan rumus yang sudah kalian
kenal? Tentu saja tidak. Daerah atau bangun datar pada Gambar 2.
merupakan bangun datar yang dibatasi kurva y = f(x), sumbu X, serta
garis x = a dan y = b.
Untuk memahami pengertian integral sebagai luas suatu bidang datar,
perhatikan Gambar 2. Daerah yang diarsir adalah suatu daerah yang
dibatasi kurva y = f(x) dan sumbu X dari a sampai b. Dimisalkan fungsi y
= f(x) terdefinisi pada interval tertutup [a, b].
Bagilah interval tertutup tersebut menjadi n buah subinterval yang sama lebar sehingga terdapat n buah titik tengah, yaitu x1, x2,
x3, ..., xn, dengan x1 = ½ (t0
+ t1), x2 = ½ (t1 + t2), ..., xn
= ½ (tn–1 + tn) (perhatikan Gambar 3). Dimisalkan ujung paling kiri interval adalah t0 = a dan ujung paling kanan adalah tn = b dengan a < t1 < t2
... < tn–1 < b.
 |
| Gambar 3. Interval tertutup tersebut menjadi n buah subinterval yang sama lebar sehingga terdapat n buah titik tengah. |
Misalkan panjang tiap subinterval adalah ti – ti–1
= ∆x. Pada tiap
subinterval [ti–1, ti], tempatkan sebuah titik x (tidak harus di tengah, boleh sama dengan titik ujungnya).
Domain fungsi y = f(x) dibagi menjadi n buah subinterval dengan alas ∆x dan tinggi f(xi) sehingga membentuk pias-pias persegi panjang. Luas masing-masing persegi panjang adalah f(xi) ∆x. Jika semua luas persegi panjang dijumlahkan maka diperoleh :
J = f(x1) ∆x + f(x2) ∆x +
f(x3) ∆x + ... +f(xn) ∆x .
J = (f(x1) + f(x2) + f(x3)
+ ... + f(xn)) ∆x
J =
dengan Σ merupakan
notasi jumlah yang berurutan. J disebut dengan jumlahan Riemann. Notasi
ini pertama kali digunakan oleh Bernhard Riemann.
 |
| Gambar 4. Jumlahan Riemann itu mendekati luas daerah yang diarsir. |
Jika banyak pias n mendekati tak berhingga (n → ∞), jumlahan Riemann itu mendekati luas daerah dari Gambar 4. Oleh sebab itu, luas L dapat ditulis dalam bentuk :
L = 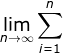 f (xi) ∆x ............................................. (1)
f (xi) ∆x ............................................. (1)
Jika n → ∞ maka ∆x → 0.
Integral tertentu f dari a sampai b dinyatakan dengan 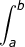 f (x) dx dan oleh Riemann nilainya didefinisikan sebagai :
f (x) dx dan oleh Riemann nilainya didefinisikan sebagai :
Dari definisi integral tertentu di atas dapat dikatakan 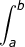 f(x) dx menyatakan luas daerah yang dibatasi oleh garis x = a, garis x = b, kurva y = f(x), dan sumbu X.
f(x) dx menyatakan luas daerah yang dibatasi oleh garis x = a, garis x = b, kurva y = f(x), dan sumbu X.
 |
| Gambar 5. luas daerah yang dibatasi oleh garis x = a, garis x = b, kurva y = f(x), dan sumbu X. |
Perhatikan bahwa substitusi (1) dan (2) menghasilkan :
L = 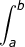 f (x) dx ........................................................... (3)
f (x) dx ........................................................... (3)
Sekarang kita misalkan ʃ f (x) dx = F(x) + c. Luas L di atas merupakan fungsi dari x dengan x ϵ [a, b] berbentuk :
L(x) = 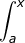 f (x) dx = F(x) + c
f (x) dx = F(x) + c
Jika nilai t ada pada interval [a, b], yaitu {x | a ≤ x ≤ b} kita dapat mendefinisikan luas L sebagai fungsi dari t berbentuk :
L(t) = 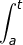 f (x) dx = F(t) + c
f (x) dx = F(t) + c
Akibat dari pemisalan di atas, akan diperoleh :
L(a) =  f (x) dx = F(a) + c = 0.
f (x) dx = F(a) + c = 0.
Sebab luas daerah dari x = a hingga x = a berbentuk ruas garis sehingga
luasnya sama dengan nol. Karena L(a) = 0 maka diperoleh :
F(a) + c = 0 atau c = –F(a) ..................... (4)
Akibat lain dari pemisalan itu, akan diperoleh
L(b) = 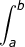 f (x) dx = F(b) + c ................... (5)
f (x) dx = F(b) + c ................... (5)
Hasil substitusi dari persamaan (4) ke (5), diperoleh :
L(b) = 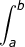 f (x) dx = F(b) – F(a)
f (x) dx = F(b) – F(a)
Dengan demikian, dapat disimpulkan bahwa jika L adalah luas daerah yang
dibatasi oleh kurva y = f(x), sumbu X, garis x = a dan garis x = b maka :
L = 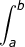 f (x) dx = F(b) – F(a)
f (x) dx = F(b) – F(a)
2. Pengertian Integral Tertentu
Kalian tahu bahwa :
menyatakan luas daerah yang dibatasi oleh kurva y = f(x), sumbu X, garis x = a, dan garis x = b.
Misalkan f kontinu pada interval tertutup [a, b] atau a ≤ x ≤ b.
Jika F suatu fungsi sedemikian rupa sehingga F'(x) = f(x) untuk semua x pada [a, b], berlaku :
Jika F suatu fungsi sedemikian rupa sehingga F'(x) = f(x) untuk semua x pada [a, b], berlaku :
F(x) adalah antiturunan dari f(x) pada a ≤ x ≤ b.
Menggambar Daerah yang Dibatasi oleh Kurva
Tentu kalian masih ingat bagaimana menggambar grafik fungsi linear, fungsi kuadrat, maupun fungsi trigonometri. Grafik fungsi-fungsi tersebut banyak dibahas di sini, berkaitan dengan pencarian luas daerah yang batasi oleh kurva. Bagaimana cara menggambarkan daerah itu? Misalkan kita akan menggambar daerah yang dibatasi oleh kurva f(x) = x dari x = 0 sampai x = 2, sumbu X, dan garis x = 2.
Langkah pertama adalah menggambar grafik f(x) = x.
Kemudian, tarik garis batasnya, yaitu dari x = 0 sampai x = 2 hingga memotong kurva. Arsir daerah yang berada di bawah kurva f(x) = x dari x = 0 sampai x = 2 dan di atas sumbu X. Hasilnya tampak seperti gambar di bawah ini.
 |
| Gambar 6. Menggambar Daerah yang Dibatasi oleh Kurva. |
Bagaimana jika daerah yang akan digambar dibatasi oleh dua kurva? Pada
dasarnya sama dengan cara di atas. Misalkan kita akan menggambar daerah
yang dibatasi oleh grafik f(x) = x dan g(x) = 2x dari x = 0 sampai x = 2
dan garis x = 2.
Terlebih dahulu, kita gambar f(x) = x dan g(x) = 2x pada bidang koordinat. Tarik garis batasnya, yaitu x = 0 dan x = 2 hingga memotong kedua grafik. Kemudian, arsir daerah yang dibatasi oleh grafik itu dari x = 0 sampai x = 2. Hasilnya tampak seperti gambar di samping.
Cobalah kalian gambar daerah yang dibatasi oleh kurva-kurva berikut.
1. f(x) = x2 dan sumbu X
2. f(x) = x2 dan g(x) = x
3. f(x) = x2 dan g(x) = x3
Contoh Soal 7 :
Tentukan integral tertentu untuk menghitung luas daerah yang diarsir pada gambar-gambar berikut.
 |
| Gambar 7. Menghitung luas daerah yang diarsir menggunakan integral tertentu. |
Kunci Jawaban :
a. Gambar 7 (a) merupakan grafik garis lurus yang melalui titik (0, 3) dan (3, 0) maka persamaan garisnya adalah x + y = 3 atau y = 3 – x. Untuk batas kiri adalah sumbu Y, berarti x = 0 dan batas kanan adalah x = 3. Jadi, luas daerahnya dapat dinyatakan dengan
b. Gambar 7 (b) merupakan suatu daerah yang dibatasi oleh sumbu X dan
kurva y = f(x). Karena kurva memotong sumbu X di titik (0, 0) dan (6, 0)
maka y = 6x – x2. Untuk batas kiri adalah garis x = 2 dan batas kanan adalah x = 4. Jadi, luas daerahnya dapat dinyatakan dengan 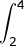 (6x - x2) dx.
(6x - x2) dx.
Contoh Soal 8 :
Gambarkan daerah-daerah yang luasnya dinyatakan dengan integral berikut.
a. 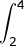 (x + 2) dx
(x + 2) dx
b.  (4 - x2) dx
(4 - x2) dx
Pembahasan :
a. Grafik y = f(x) = x + 2 mempunyai titik potong (0, 2) dan (–2, 0) sehingga 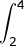 (x + 2) dx dapat digambarkan seperti pada Gambar 8.
(x + 2) dx dapat digambarkan seperti pada Gambar 8.
 |
| Gambar 8. Grafik y = f(x) = x + 2. |
b.  (4 - x2) dx
(4 - x2) dx
Diketahui f(x) = 4 – x2 dengan batas bawah x = 0 dan batas atas x = 2. Kurva f(x) = 4 – x2 merupakan
parabola dengan titik potong (–2, 0) dan (2, 0) yang membuka ke bawah.
Dengan demikian, daerah tersebut dapat digambarkan seperti pada Gambar
9.
 |
| Gambar 9. Kurva f(x) = 4 – x2 |
Contoh Soal 9 :
Tentukan nilai-nilai integral berikut.
a. 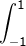 (x + 3) dx
(x + 3) dx
b. 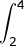 (x3 - x) dx
(x3 - x) dx
Penyelesaian :
3. Sifat-Sifat Integral Tertentu
Integral sebenarnya dapat ditentukan dengan mudah. Untuk mempermudah perhitungan integral, kalian dapat memanfaatkan sifat-sifat integral. Agar kalian menemukan sifat-sifat integral, perhatikan contoh-contoh berikut.
Contoh Soal 10 :
Hitunglah nilai integral dari fungsi berikut.
a.  (2x + 4) dx
(2x + 4) dx
b.  (3x2 + 4) dx
(3x2 + 4) dx
c.  (3x2 + 4) dx
(3x2 + 4) dx
Jawaban :
Contoh Soal 12 :
Tentukan nilai-nilai integral berikut.
a. 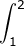 6x2 dx
6x2 dx
b. 6 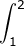 x2 dx
x2 dx
c.  (5x4 + 2x) dx
(5x4 + 2x) dx
d.  5x4 dx +
5x4 dx +  2x dx
2x dx
e. Dari nilai integral pada bagian a sampai dengan d tersebut, apa yang dapat kalian simpulkan dari hubungan tersebut?
Penyelesaian :
Contoh Soal 13 :
a. 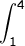 4x3 dx
4x3 dx
b. 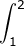 4x3 dx +
4x3 dx + 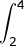 4x3 dx
4x3 dx
c. Dari hasil a dan b, apa kesimpulan kalian?
Dari contoh-contoh di atas maka dapat dituliskan sifat-sifat integral sebagai berikut.
Misalkan f(x) dan g(x) adalah fungsi-fungsi kontinu pada [a, b], berlaku sebagai berikut.
a.  f (x) dx = 0
f (x) dx = 0
b. 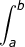 c f (x) dx = c
c f (x) dx = c 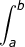 f (x) dx , dengan c = konstanta
f (x) dx , dengan c = konstanta
c. 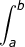 f (x) dx = -
f (x) dx = - 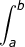 f (x) dx
f (x) dx
d. 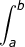 [ f (x) ± g(x)] dx =
[ f (x) ± g(x)] dx = 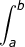 f (x) dx +
f (x) dx + 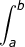 g(x) dx
g(x) dx
e. 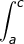 (x) dx +
(x) dx + 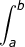 f (x) dx =
f (x) dx = 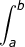 f (x) dx, dengan a ≤ c ≤ b
f (x) dx, dengan a ≤ c ≤ b
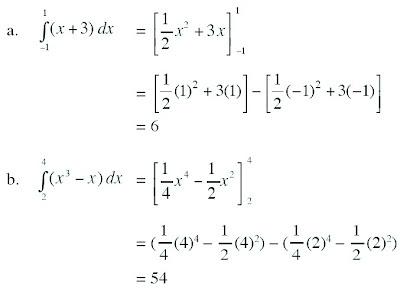



Tidak ada komentar:
Posting Komentar